HOW TO CALCULATE CUTTING LENGTH OF TRIANGLE STIRRUPS

HOW TO CALCULATE CUTTING LENGTH OF TRIANGLE STIRRUPS IN BEAM AND COLUMN

A stirrup is a closed loop of reinforcement bar that is used to hold the main reinforcement bars together in an RCC structure. In a column, the stirrups provide the lateral support to the main bars against buckling.

Different Shapes of Stirrups

1)     Rectangular Stirrups

2)     Square Stirrups

3)     Circular Stirrups

4)     Triangular Stirrups

5)     Spiral Stirrups

6)     Diamond Stirrups

Types Of Stirrups Used In Beam And Columns

1)     Single Legged Stirrups(Open stirrup)

2)     Two-legged or Double Legged Stirrups (Closed Stirrup)

3)     Four-legged Stirrups (Closed Stirrup)

4)     6-legged Stirrups (Closed Stirrup)

Steps involved in finding the cutting length of stirrups

1)     Look at the size of column or beam from drawings

2)     Adopt Dia of the bar (generally 8mm Dia is used for stirrups)

3)     Deduct the concrete cover or clear cover

4)     Find the total outer length of stirrup after deducting concrete cover.

5)     Add the length of the hook to the length of the stirrup

6)     Deduct the length of bends

7)     Use below formula to find the total cutting length of stirrups

Formula To Find The Total Cutting Length Of Stirrups

Cutting Length of Stirrups = Perimeter of Shape + Total hook length – Total Bend Length

PERIMETER OF SHAPE

Perimeter of Rectangle = 2 ( length + breadth)

Perimeter of Square = 4 x side length

Perimeter of circle or Circumference of Circle = 2πr = πd

(r= radius, d= Diameter of Circle)

Perimeter of triangle = a²=b²+c² (we are using pythagorean theorem to find its length)

TOTAL HOOK LENGTH

1 Hook length = 9d or 75mm

TOTAL BEND LENGTH

45° Bend length = 1d

90° Bend length = 2d

135° Bend length = 3d (Remember, d = Diameter of Bar)

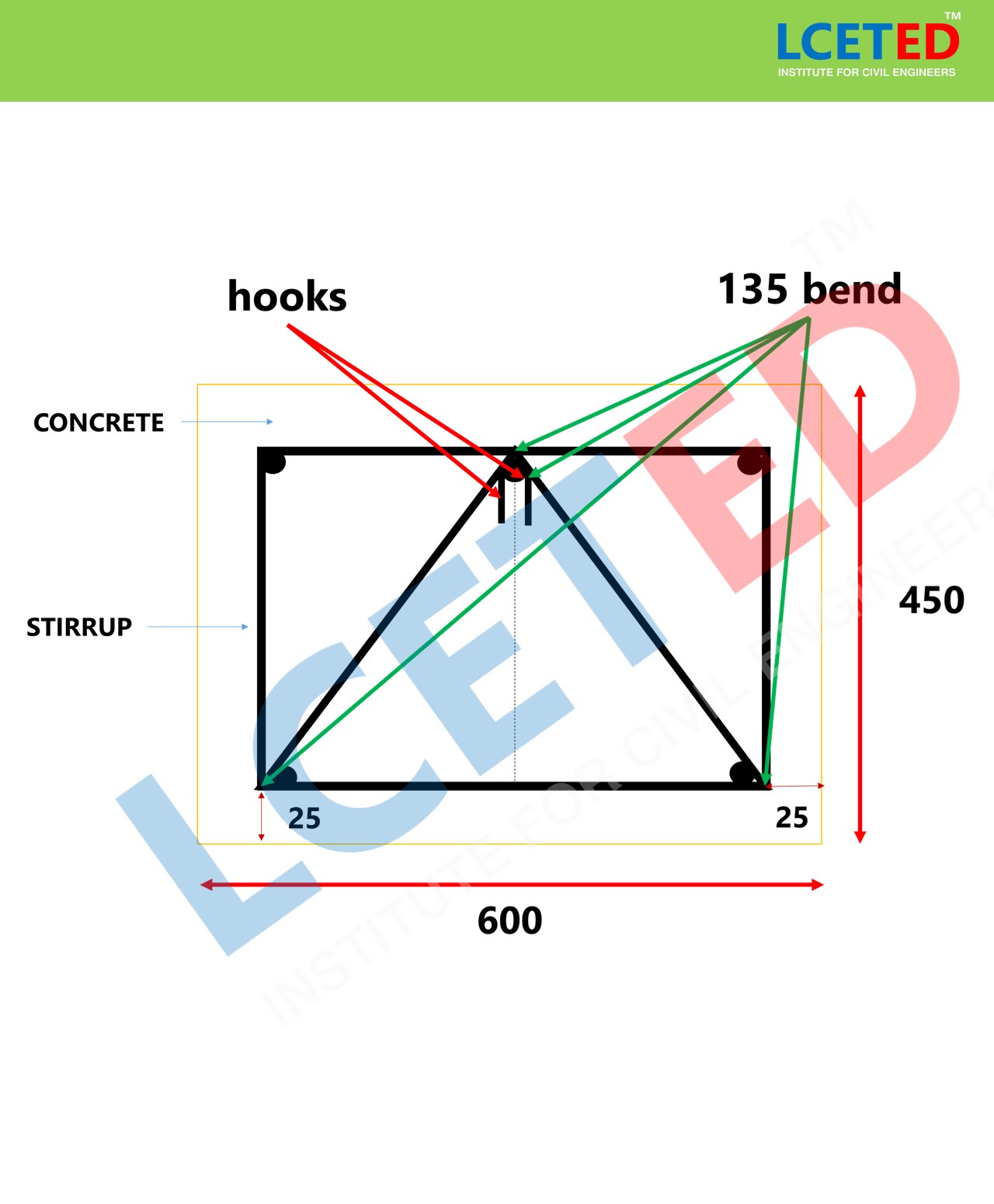
Cutting Length of Triangle Stirrups

Cutting Length of Stirrups = Perimeter of Shape + Total hook length – Total Bend Length

Cutting Length of Square Stirrup = ((2 x H) + “A” side) + 2 numbers of hooks – 4 numbers of 135° bends

H = hypotenuse side of triangle

EXAMPLE TRIANGLE STIRRUP CALCULATION

-
1. the column size as 600mm x 450mm

2. Adopting Dia of Bar used for stirrups is 12mm (d=12mm)

3. Deducting the concrete cover 25mm from all sides (in the all sides are equal)

A = 600  - 25 -25 = 550 mm

b = 450 -25 -25 = 400 mm

   

4. Total Length of the hook:
There are 2 hooks which mean 9d+9d = 18d

5.   Total Length of Bends:
There are 4 bends which are bent at an angle of 135⁰ because of triangle stirrup

6. Total Cutting Length Of Triangle Stirrup = ((2 x H) + “A” side) + 2 numbers of hooks – 4 numbers of 135° bends

= ((2 x H) + “A” side) + 2(9d) – 4 (3d)

For this we need to find H (Hypotenuse) length. So, we use Pythagorean Theorem to find it

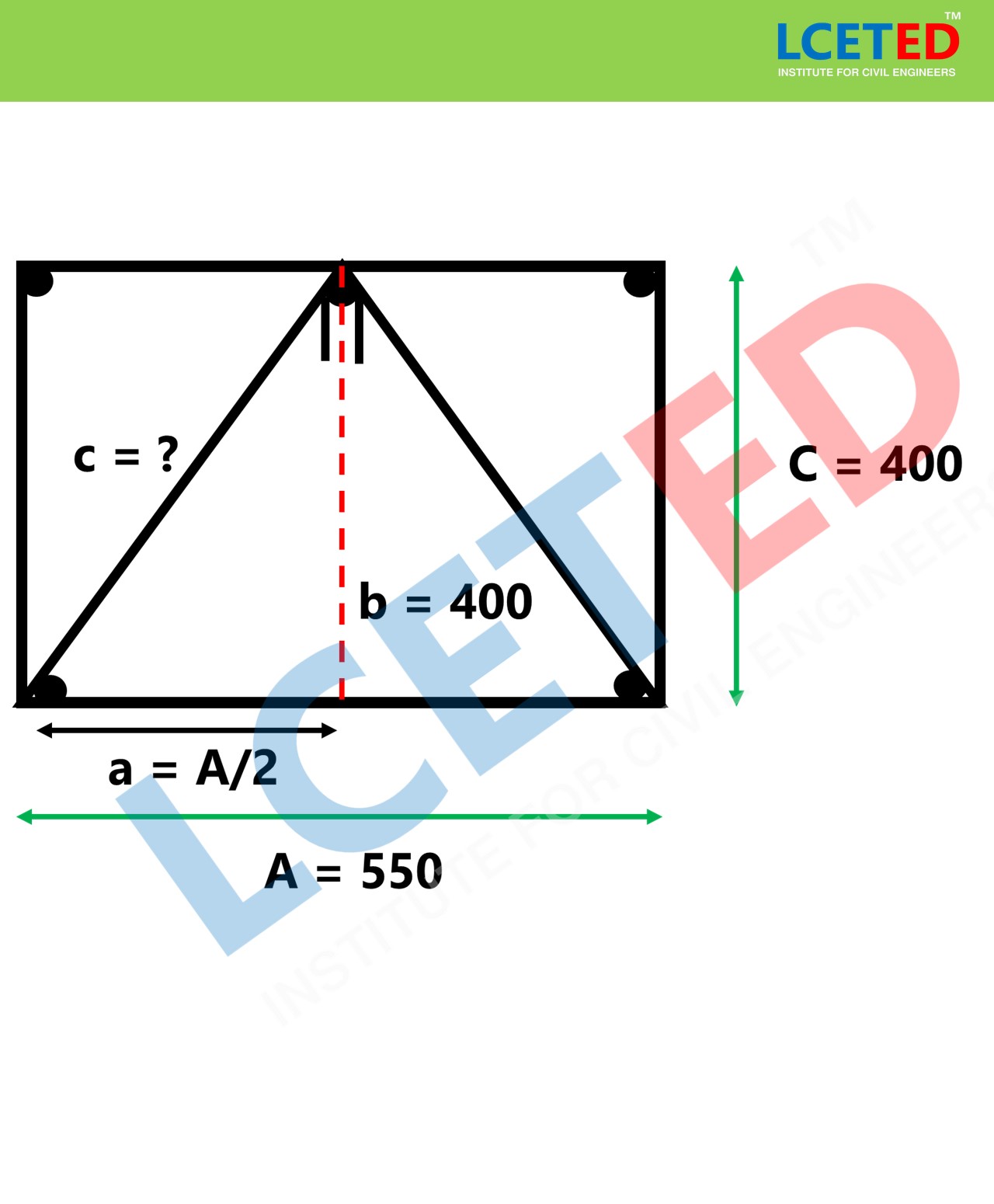
Consider H = c, to applying it in the formula

As we know A = 550

To find c,

We Use Pythagorean Theorem = a² + b² = c²

c = √(a² + b²)

a= A/2 =550/2 =225, b= 400

We substitute in formula

c = √(225² + 400²) = 458.93

c= H = 458.93mm

now, we can substitute these values in the Cutting Length Of Triangle Stirrup formula

= ((2 x H) + “A” side) + 2(9d) – 4 (3d))

H = 458.93

A = 550

d = dia of stirrup = 8

= ((2 x 458.93) + 550) + 2(9x8) – 4 (3x8))

= 1515.86mm = 1.51m

Cutting Length Of Triangle Stirrup = 1515.86mm = 1.51m

Also Read: All You Want To Know About Stirrups In Beam And Column

Also Read: How to Calculate Cutting Length For Square Stirrups

Also Read: How to Calculate Cutting Length Of Circle Stirrups In Beam And Column

Also Read: How to Calculate Cutting Length For Spiral Stirrups

-

HOPE YOU LIKE THIS ARTICLE SUBSCRIBE US OR CLICK THE BELL ICON FOR INSTANT NOTIFICATION

LCETED INSTITUTE FOR CIVIL ENGINEERS

“Our Mission To Educate And Keep People Informed By Creating A Trusted Source Of Knowledge Everything Related To Civil Engineering”. 

PRESS THE BELL ICON TO FOR THE NOTIFICATION

Share