How To Make BBS Of Pile Foundation & Pile Cap - LCETED

 

In this article, we explained How to make a bar bending schedule of pile foundation

PILE FOUNDATION DIAGRAM

 

 

GIVEN DATA:

 

 

Pile cap length = 4000mm

Pile cap breadth= 4000mm

Pile diameter = 1.2m or 1200mm

Pile radius = 0.5m or 500mm

Number of Vertical rod in piles = 16nos

Length of the pile driven = 32.5m

Clear cover of the pile= 75mm

 

Vertical Rods Diameter and Numbers of Piles

Length	No of vertical rods are used in piles	Diameter of steel
0 to -12 m	16nos	25Ø
-12 to -21m	16nos	20Ø
-21 to -32.5m	16nos	16Ø

 

The length of the vertical rods, divided by 12meter of rod length and diameter of the rod changes on each segment, which will be decided by the structural consultant. The above table is for calculation purpose

 

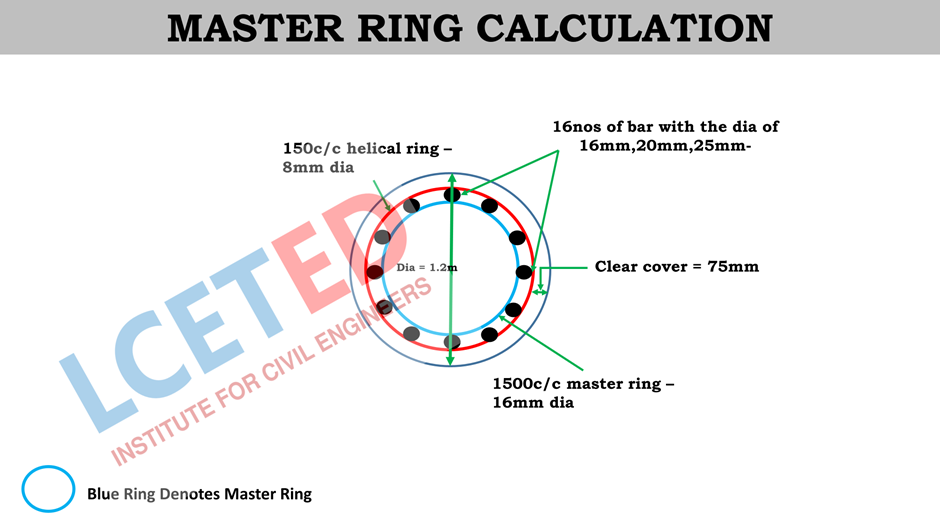
Master Ring Calculation

Dia. Of master ring = 16 mm @ 1500 mm c/c

No. of master ring = (Length of pile / Spacing) + 1 = 32.5/1.5 = 21.67 = 22nos

 

Helical Ring Calculation

No. of spirals = (Length of pile / Pitch of pile) + 1 = 32.5/0.15 = 216.67 = 217nos

 

MASTER RING CALCULATION

 

Details Given for Master Ring

Length of pile = 32.5 m or 32500 mm

Diameter Of master ring = 16 mm @ 1500 mm c/c

 

Length of 1 master ring = Circumference of ring/circle = 2 πr

r = R = Radius = diameter/2

Diameter of The Master Ring = Diameter of pile – (2 x clear cover) – (2 x spiral ring diameter) – (2 x Vertical bar diameter) – (Master ring dia)

Vertical bar diameter varies in each segment as 16, 20 and 25. We will take 25mm dia for the vertical bar diameter because it is the highest dia

 

Dia = 1200 – (2x75) – (2x8) – (2x25) – (16)

Dia = 968mm

r = dia/2 = 968/2 = 484mm = 0.484m

 

Length of 1 master ring = Circumference of circle = 2 πr

Length of 1 master ring = 2 x 3.14 x 0.484 = 3.039m

 

Total number of master ring (N_r)= (Length of pile / Spacing) + 1 = (32500 / 1500) + 1 = 22.67 - 23nos.

 

For 23 nos. of master ring = 3.039 x 23 = 69.897m of 16mm dia

 

SPIRAL OR HELICAL RING CALCULATION

 

 

Details Given For Spiral or Helical Ring:

 

Dia. of pile = 1200 mm or 1.2 m

Length of pile = 32.5 m or 32500 mm

Pitch or Spacing = 150 mm

Clear cover = 75 mm

Dia. of spiral bar = 8 mm Ø

 

Length of 1 helical ring = Circumference of ring/circle= 2 πr

r = R = Radius = diameter/2

Diameter of the helical Ring = Diameter of the pile – (2 x clear cover) – (Spiral bar dia)

Diameter of the helical Ring = 1200 – (2x75) – (8) = 1042mm

Diameter = r/2 = 1042mm

r = dia/2 = 1042/2 = 521mm

r = 521mm or 0.521mm

 

Length of 1 spiral or helical ring = 2πr = 2 x π x 0.521 = 3.27mm

 

No. of helical or spirals ring (N_r) = (Length of pile / Pitch of pile) + 1

= (32500 / 150) + 1

= 217.666666667 – 218 nos.

 

Total length of spiral or helical ring = 3.27 x 218 = 712.86m

 

We know that the length of a full-length bar is 12 m. so, we should find the total length of lap

 

To find, Lap considered 50 d

As we know diameter of spiral ring 8mm = 50 x 8 = 400 mm = 0.4 m

 

Number of lap needed = [Total no. of bar / One full length bar] – 1

= (712.86 / 12) – 1 = 58.405 – 59nos

 

Total length of lap = 0.4 x 59 = 23.6 m

 

Total Length of Spiral Ring = 712.86m + 23.6m = 736.46 meters of 8mm dia

 

VERTICAL BAR CALCULATION

Details Given on Vertical Bar Calculation

 

Length of one bar 25 ф – 12m

Length	No vertical rods used in piles	Diameter of steel
0 to -12 m	16nos	25Ø

 

= 50 d +12000 + 50d = (50 x 25) + 12000 + (50 x 25) = 14.5 m - 14500 mm

Therefore,

Length for 16 no. bar = 14.5 x 16 = 232m

 

Length of one bar 20 ф – 12m

Length	No of vertical rods are used in piles	Diameter of steel
-12 to -21m	16nos	20Ø

 

= 50 d +12000 = (50 x 25) + 12000 = 13.25 m - 13250 mm

Therefore,

Length for 16 no. bar = 13.25 x 16 = 212m

 

 

Length of one bar 16 ф – 8.5m

Length	No of vertical rods are used in piles	Diameter of steel
-21 to -32.5m	16nos	16Ø

 

= 8500 + 300 – (bend) = 8500 + 300 – (2d) = 8500 + 300 – (2x16) = 8.768m - 8768mm 

Therefore,

Length for 16 no. bar = 13.25 x 8.768 = 116.176m

 

Dia. of bar in mm	Spiral ring	Master ring	Vertical rod	Total length in m	Unit weight of steel in kg/m	Total weight in kg
8 mm	736.46 m	-	-	736.46 m	0.395 kg/m	290.90 kg
16 mm	-	69.897m	116.176m	186.07m	1.58 kg/m	293.99 kg
20 mm	-	-	212m	212 m	2.47 kg/m	523.64 kg
25 mm	-	-	232m	232 m	3.86 kg/m	895.52 kg
Total Weight in Kg						2004.05

 

 

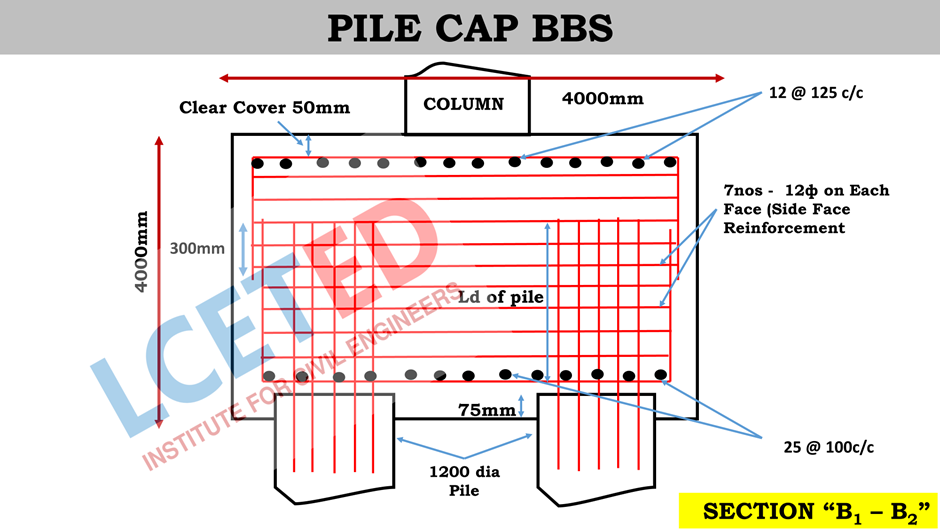
How to Make BBS of Pile Cap - Pile Cap Steel Bar Calculation

 

Given Details

Pile Cap size = 4.0m x 4.0m

 

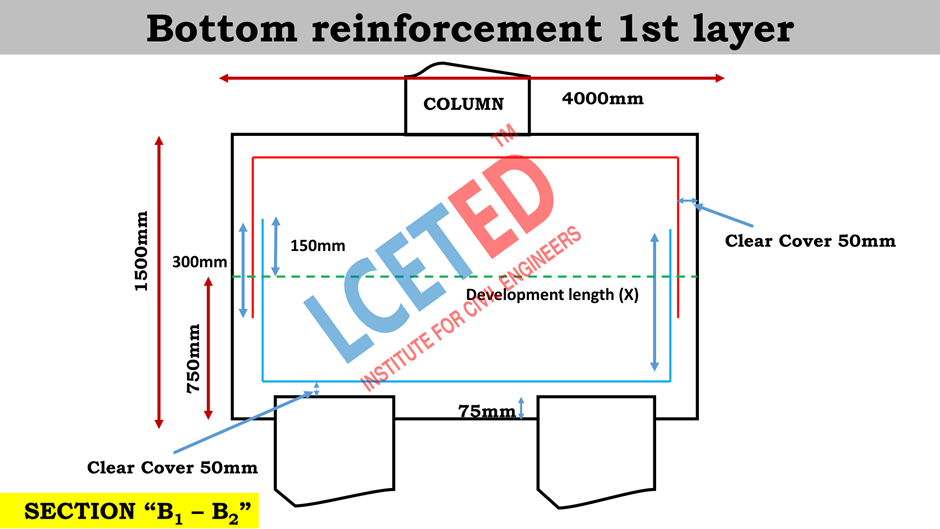
Bottom Reinforcement 1st layer

 

Pile Cap Size = 4000 X 4000

Clear cover = 50 mm

Bottom reinforcement dia = 25 ф

 

Length of the Bottom reinforcement 1st layer = Length of pile cap – (2 x clear cover) – (2 x half of dia bar) + (2 x development length (x)) – (2 x bend)

As we know,

Clear cover = 50mm

Diameter = 25mm

Bend = 2d = 2 x 25 = 50mm

Development length x = 750 – 75 – 50 (clear cover) – 12.5 (half dia) + 150 = 762.5mm – 0.762m

 

Therefore,

Length of the Bottom reinforcement 1st layer = 4000 – (2 x 50) – (2 x 25/2) + (2 x 762.5) – (2 x 50) = 5300 mm = 5.3m

 

Number of bar (25 ф @ 100c/c) = [Length of bar / Spacing] + 1 = [4000 / 100] + 1 = 41 nos.

For 41 nos,

 

Total length of bar required = 5.3 x 41 = 217.3m

 

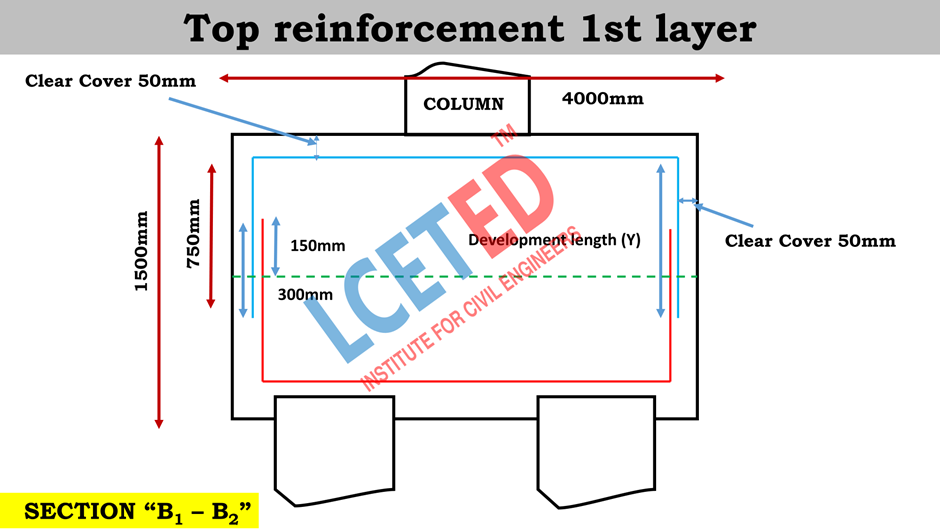
Top Reinforcement 1st layer

 

Length of the Top reinforcement 1st layer = Length of pile cap – (2 x clear cover) – (2 x half of dia bar) + (2 x development length (x)) – (2 x bend)

As we know,

Clear cover = 50mm

Diameter = 12mm

Bend = 2d = 2 x 12 = 24mm

Development length Y = 750 – 50 (clear cover) – 6 (half dia) + 150 = 844mm – 0.844m

 

Therefore,

Length of the Top reinforcement 1st layer = 4000 – (2 x 50) – (2 x 12/2) + (2 x 844) – (2 x 24) = 5528mm = 5.5m

 

Number of bar (12 ф @ 125 c/c) = [Length of bar / Spacing] + 1 = [4000 / 125] + 1 = 33 nos.

For 33 nos,

 

Total length of bar required = 5.5 x 33 = 181.5m

 

 

Bottom Reinforcement 2nd layer

 

 

Length of the Bottom reinforcement 2_nd layer 25 ф = Length of pile cap – (2 x clear cover) – (2 x half of dia bar) + (2 x development length (x₁)) – (2 x bend)

As we know,

Clear cover = 50mm

Diameter = 25mm

Bend = 2d = 2 x 25 = 50mm

Development length X₁ = 750 – 75 – 50 (clear cover) – 12.5 (half dia) – 25 (1^st reinforcement dia) + 150 = 737.5mm – 0.737m

 

Therefore,

Bottom reinforcement 2_nd layer 25 ф = 4000 – (2 x 50) – (2 x 25/2) + (2 x 737.5) – (2 x 50) = 5250mm – 5.2m

 

Number of bar (25 @ 100 c/c) = [Length of bar / Spacing] + 1 = [4000 / 100] + 1 = 41 nos.

For 41 nos,

 

Total length of bar required = 5.2 x 41 = 213.2m

 

Top Reinforcement 2nd layer

 

Length of the Top reinforcement 2_nd layer 12 ф = Length of pile cap – (2 x clear cover) – (2 x half of dia bar) + (2 x development length (Y₁)) – (2 x bend)

As we know,

Clear cover = 50mm

Diameter = 12mm

Bend = 2d = 2 x 12 = 24mm

Development length Y₁ = 750 – 50 (clear cover) – 6 (half dia) – 12 (1^st reinforcement dia) + 150 = 832mm – 0.832m

 

Therefore,

Top reinforcement 2_nd layer 12 ф = 4000 – (2 x 50) – (2 x 12/2) + (2 x 832) – (2 x 24) = 5504mm – 5.5m

 

Number of bar (12 ф @ 125 c/c) = [Length of bar / Spacing] + 1 = [4000 / 125] + 1 = 33 nos.

For 33 nos,

 

Total length of bar required = 5.5 x 33 = 181.5m

 

Side Face Reinforcement

Length of the Side reinforcement 12 ф = (Length of pile cap – (2 x clear cover) – (2 x half of dia bar) + (2 x development length) – (2 x bend)) x 2 (sides)

As we know,

Clear cover = 50mm

Diameter = 12mm

Bend = 2d = 2 x 12 = 24mm

Development length Y₁ = 2000 – 50 (clear cover) – 6 (half dia) –+ 150 = 2094mm – 2.094m

 

Therefore,

Length of the Side reinforcement 12 ф = (4000 – (2 x50) – (2 x 6) + (2 x 2094) – (2 x 24)) x 2 = 16056mm - 16m

 

Number of bar (12 @ 125 c/c) = [Length of bar / Spacing] + 1 = [2000 / 125] + 1 = 17 nos.

For 17 nos,

 

Total length of bar required = 16 x 17 = 272m

 

Dia. of bar in mm	Spiral ring	Master ring	Vertical rod	Side reinforcement	Top reinforcement	Total length in m	Unit weight of steel in kg/m	Total weight in kg
8 mm	736.46 m	-	-	-	-	736.46 m	0.395 kg/m	290.90 kg
12 mm	-	-	-	272m	363m	635 m	0.889 kg/m	564.51 kg
16 mm	-	69.897m	116.176m	-	-	186.07m	1.58 kg/m	293.99 kg
20 mm	-	-	212m	-	-	212 m	2.47 kg/m	523.64 kg
25 mm	-	-	232m	-	430.5m	662.5 m	3.86 kg/m	2557.25 kg

 

Total weight of steel required = 4230.29/kg - 4.2ton

 

 

 If you find 

This information is helpful, please share it.

 

Thanks! For reading the article... 

Tags: #pilefoundations #pilefoundaitonbbs #foundationpiles #foundationdrilling #deepfoundation #pilefoundation #piling #corebarrel #bulletteeth #rollerbits #boredpiling #drillrig #drillingbucket #boredpiles #boredpile #foundationcontractor #rockdrilling #pilingrig #drillingtools #rockbucket #pilings #deepfoundationdrilling #foundationdrillingtools #corebarreldrilling #hardrockdrilling #pilingequipment #rockdrillingtools #pilingrigs #pilingworks #deepfoundations #pilingwork