All You Want Know About Cantilever Beams | Civil Engineering | LCETED

Cantilever beams are elements that are supported at one end and carry a load at the other end or are distributed along the unsupported part. To ensure that the structure is static, the support must be fixed, which means that it can withstand forces and moments in all directions.

The upper half of the cantilever beam thickness is subjected to tensile stress, tendency to elongate the fibers, the lower half to compressive stress, tendency to crush them. Beams may be raised outside their supports by a distance equal to a quarter of the span between supports.

Cantilevers deflect more than most other types of beams because they only rest at one end. This means that there is less support for the load to be transferred. 

A great example of a cantilever beam is a balcony. A balcony is only supported at one end, the rest of the beam runs over open space; there is nothing to support it on the other side.

This structural beam is widely used in the construction of bridges, towers and buildings and can add a unique charm to the structure.

This article, explains some important structural steps and basic concepts of a cantilever beam in construction.

 

How to calculate Cantilever beam deflection?

Cantilever beam deflection can be calculated in different ways, for example with simplified cantilever beam equations or calculators and cantilever software.

 

 

Structural Behaviour of Cantilever Beam

As shown in Fig-2 below, a cantilever beam bends downwards when subjected to vertical loads. A cantilever beam can be subjected to

·       Point load,

·       Uniform load

·       Varying load

 

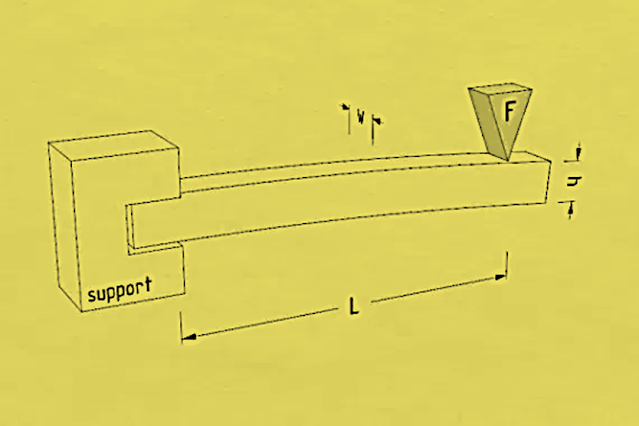Fig--2: Cantilever Beam Bending Downwards Due to a Load 'F' at Free End

Regardless of the type of load, it bends downward creating an upward convexity. This flexion creates tension in the upper fiber and compression in the lower fibres. Therefore, the main reinforcement is provided to the upper fiber of the concrete beam, because there is a high tensile stress as shown in Fig 4.

 

Cantilever Beam - Shear Force (SF) and Bending Moment (BM) Diagram

The shear force of any part of a cantilever beam is the sum of the loads between the section and the free end. The moment of bending in a given section of a cantilever beam is the sum of each moment according to the section of all loads acting between the section and the free end.

Consider,

Cantilever beam AB of length 'l' subjected to a point load 'W' at the end B.

A section X-X at a distance 'x' from the free end B is placed.

The shear force at section X-X is Rx, which is equal to W and the bending moment of section X-X is Mx, which is equal to W.x.

 

Fig-3: Bending and Shear Force Diagram of Cantilever Beam with Point Load at Free End

The shear force at fixed support A is determined by holding the part at A,

Which gives the shear force Ra=W; and

Moment Ma = W.l.

Based on which the shear force and bending moment diagram are developed.

The cantilever beam has a maximum bending moment at the fixed end and decreases to zero at the free end. The diagram of bending and shear forces is determined for all possible load combinations in order to design a cantilever beam for a structure. The load applied to the beam is a combination of dead load and live loads in accordance with design standards.

 

Cantilever Beam Design

A cantilever beam is subjected to moment and shear stresses under the action of structural loads. The purpose of any design process is to safely transfer these stresses to support.

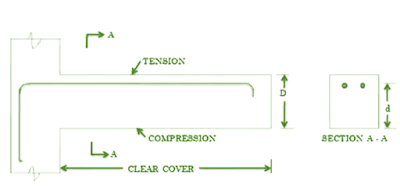Figure-4: Structural Behavior of Cantilever Beam

The cantilever beam has a bending moment that varies from zero at the free end to the maximum value at the fixed end support (Fig- 3). Therefore, when designing the cantilever beams, the main reinforcement is provided to the upper beam of the concrete beam to safely resist the tensile stress.

 

The maximum spacing of a cantilever beam generally depends on the following factors:

·        Depth of cantilever

·        Load size, type and location

·        Quality and type of materials used

 

Generally, for small cantilever beams, the span is limited to 2 to 3 m. But the depth can be increased to increase the span or by using a steel or pre-pressed structural unit. This structure can last a long time because it can be safely shifted to the ground in the face of the moments created by the cantilever. Detailed analysis and design of the structure will help to explore the feasibility of cantilever beams at long intervals.

 

The cantilever beam must be properly fixed or supported against the wall to minimize the inverse effect.

 

Uses of Cantilever Beam in Construction

Cantilever beam elements are used in the following applications:

·       Construction of cantilever beams and balconies

·       Temporary cantilever support structures

·       Freestanding radio towers without guy-wires

·       Pergolas construction

·       Construction of lintel in buildings

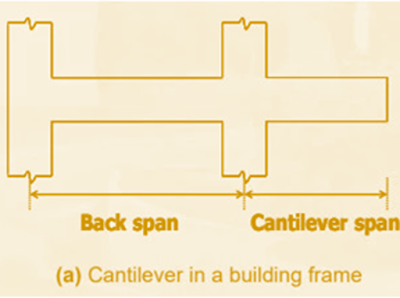Fig-5: Applications of Cantilever Beam in Buildings and Bridge Girders

·       In building construction, there are various applications such as the cantilever beam, i.e. gallery, roof, upward crane runway, or part of a building above and the sun shed, shelves, large halls, exhibition buildings and weapons.

 

ADVANTAGES OF CANTILEVER BEAM:

This beam has the following advantages;

·       In construction, these beams are simple.

·       On the opposite side, it does not need support.

·       This beam creates a negative bending moment, which counteracts the positive bending moment of the rear spans.

·       As the beam is inserted into the cantilever arms, the gap will be larger than a simple beam.

·       Thermal expansion and ground movement are much simpler to maintain because the beam simply rests on the hands.

·       Due to their depth, the cantilever beams are very stiff.

 

DISADVANTAGES OF CANTILEVER BEAMS

·       The cantilever beams are subjected to large deviations.

·       The cantilever beams are subjected to large moments.

·       Strong fixed support or backspan is essential to keep the structure stable

FAQs

What is a cantilever beam?

Cantilever beams are elements that are supported at one end and carry a load at the other end or are distributed along the unsupported part. To ensure that the structure is static, the support must be fixed, which means that it can withstand forces and moments in all directions.

 

What is the maximum span of cantilever beams?

Generally, for small cantilever beams, the span is limited to 2 to 3 m. But the depth can be increased to increase the span or by using a steel or pre-pressed structural unit. This structure can last a long time because it can be safely shifted to the ground in the face of the moments created by the cantilever. Detailed analysis and design of the structure will help to explore the feasibility of cantilever beams at long intervals.

 

How to calculate Cantilever beam deflection?

Cantilever beam deflection can be calculated in different ways, for example with a simplified cantilever beam equations or calculators and cantilever software.

 

How does a cantilever beam behave under loads?

a cantilever beam bends downwards when subjected to vertical loads. A cantilever beam can be subjected to

·       Point load,

·       Uniform load

·       Varying load

 

Regardless of the type of load, it bends downward, creating a pile upwards. This curve creates tension in the upper fibres and contraction in the lower fibres. Therefore, during the design of the cantilever beams, the main reinforcement is provided to the top fibre of the concrete beams to safely withstand the tensile stress.