During the survey of the alignment of a project involving roads or railways, the direction of the line may change due to some unavoidable circumstances. The angle of the change in direction is known as the deflection angle. For it to be possible for a vehicle to run easily along the road or railway track, the two straight lines (the original line and the deflected line) are connected by an arc (Fig. below) which is known as the curve of the road or track.
Curve of Road
When the curve is provided in the horizontal plane, it
is known as a horizontal
curve.
Again, the nature of the ground may not be uniform along
the alignment of any project and may
consist of different gradients (for instance, a rising gradient may be followed by a falling gradient
and vice versa). In such a case, a
parabolic curved path is provided in the vertical plane in order to
connect the gradients for easy movement
of the vehicles.
This curve is known as a Vertical curve. The following are the different forms of curves:
DEFINITIONS
AND EXPLANATIONS OF DIFFERENT TERMS
Degree of a Curve
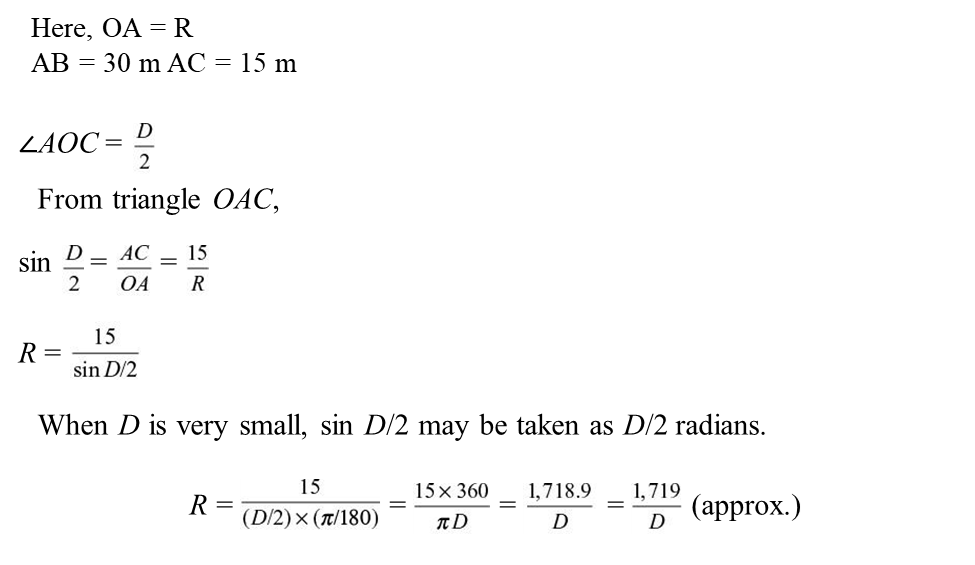
1.
Degree of Curve
The angle a unit chord of 30 m length subtends at the
centre of the circle formed by the curve
is known as the degree of the curve. It is designated as D (Fig. above).
A curve may be designated according to either the radius
or the degree of the curve.
When the unit chord subtends an angle of 1°, it is
called a one-degree curve, when the
angle is 2°, a two-degree curve, and so on.
It may be calculated that the radius of a one-degree
curve is 1,719 m.
2.
Relation between Radius and Degree of Curve
Radius and Degree of a Curve
Let AB be the unit chord of 30 m, O the centre, R the
radius and D the degree of the curve (Fig. above).
3. Superelevations
When a particle moves in a
circular path, a force (known as centrifugal force) acts upon it and tends to push it
away from the centre.
Similarly, when a vehicle
suddenly moves from a straight to a curved path, the centrifugal force tends to push the
vehicle away
from the road or
track. This is because there is no
component force to counterbalance this centrifugal force.
To counterbalance the
centrifugal force, the outer edge of the road or rail is raised to some height (with respect to the
inner edge), so that the sine component
of the weight of the vehicle (W sin θ) may counterbalance the overturning force, The height through which
the outer edge of the road or rail is
raised is known as superelevation or cant.
Superelevation
In Fig. below, P is the centrifugal force, W sin θ is
the component of the weight of the vehicle, and h is the superelevation given
to the road or rail. For equilibrium,
Where, b = width of the road in metres
G = distance between centres of rails (gauge) in metres
R = radius of the curve in metres
g = acceleration due to gravity = 9.8 m/s2
V = speed of the vehicle in metres per second
h = superelevation in metres.
4. Centrifugal Ratio
The ratio between the centrifugal force and the weight
of the vehicle is known as the centrifugal ratio.
TYPES OF HORIZONTAL CURVES
The following are the different types of horizontal
curves:
1.
Simple Circular Curve
When a curve consists of a single arc with a constant
radius connecting the two tangents, it
is said to be a circular curve (Fig. below).
Circular Curve
2. Compound Curve
When a curve consists of
two or more arcs with different radii, it is called a compound curve. Such a
curve lies on the same side of a common tangent and the centres of the
different arcs lie on the same side of their respective tangents (Fig. below).
Compound Curve
3. Reverse Curve
A reverse curve consists of
two arcs bending in opposite directions. Their centres lie on opposite sides of
the curve. Their radii may be either equal or different, and they have one
common tangent (Fig. below).
Reverse Curve
4. Transition Curve
A curve of the variable radius
is known as a transition curve. It is also called a spiral curve or easement curve. In railways,
such a curve is provided on both sides of a circular curve to minimise
superelevation. Excessive superelevation may cause wear and tear of the rail
section and discomfort to passengers
(Fig. below).
Transition
Curve
5. Lemniscate Curve
A lemniscate curve is
similar to a transition curve and is generally adopted in city roads where the
deflection angle is large. In Fig. 10.9, OPD shows the shape of such a curve.
The curve is designed by taking a major axis OD, minor axis PP′, with origin O,
and axes OA and OB. OP(ρ) is known as the polar ray and α as the polar angle.
Lemniscate Curve
TYPES OF VERTICAL CURVES
Definition
When two different
gradients meet at a point along a road surface, they form a sharp point at the apex. Unless this apex
point is rounded off to form a smooth
curve, no vehicle can move along that portion of the road. So, for the smooth and safe running of vehicles, the
meeting point of the gradients is rounded off to form a smooth curve in a vertical plane. This curve is known as a vertical curve.
Generally, the parabolic
curves are preferred as it is easy to work out the minimum sight distance in their case. The minimum sight distance is an important
factor to be considered while calculating the length of the vertical curve.
Gradient
The gradient is expressed in two ways:
a) As a percentage, e.g. 1%, 1.5%, etc.
b) As 1 in n, where n is the horizontal distance and 1 represents vertical distance, e.g. 1 in 100, 1 in 200, etc.
Again, the gradient may be ‘rise’ or ‘fall’. An up
gradient is known as ‘rise’ and is
denoted by a positive sign. A down gradient is known as ‘fall’ and is indicated by a negative sign.
Rate of Change of Grade
The characteristic of a parabolic curve is that the
gradient changes from point to point but
the rate of change in grade remains constant. Hence, for finding the length of the vertical curve, the
rate of change of grade should be an
essential consideration as this factor remains constant throughout the length of the vertical curve.
Generally, the recommended rate of change of grade is
0.1% per 30 m at summits and 0.05% per
30 m at sags.
Length of Vertical Curve
The length of the vertical curve is calculated by
considering the sight distance. To
provide minimum sight distance, a certain permissible rate of change of grade is determined and the length
of the vertical curve is calculated as
follows:
Example:
Let
us find the length of the vertical curve connecting two grades +0.5% and –0.4%
where the rate of change of grade is 0.1%.
Length
of vertical curve = (0.5-(-0.4)x30)/0.1 = ((0.5+0.4)x30x10)/1 =
0.9 x 30 x 10 = 270 m
Types of Vertical Curves
The following are the different types of vertical curves
that may occur.
(a)
Summit Curve Figure below figure shows a summit curve where an
up gradient is followed by a down
gradient.
Summit Curves
The figure below shows a summit curve where a down gradient
is followed by another down gradient.
(b)
Sag Curve: below figure shows a sag curve where a down gradient
is followed by an up gradient.
The figure below shows a sag curve where an up gradient is
followed by another up the gradient.
Sag Curves
The vertical curve may be set out by the following two
methods:
· The
tangent correction method
· The
chord gradient method
FAQ
Why Curve is Provided?
Having a straight highway or railroad in a country is practically feasible
or impossible. Some changes in the direction of their alignment are required
for terrain, culture, feature or other unavoidable reasons.
Such direction change can not be sharp but should be gradual, it
is necessary to introduce curves between straight lines.
Following a regular curved path is called a railway or highway
alignment curve.
What are the two types of
curves used in road surveys?
There are two types of
curves provided mainly
a) Horizontal
Curve
b) Vertical
Curve
What are the Types of Horizontal Curve?
Simple Curve
Compound Curve
Reverse Curve
Transition or Spiral Curve


























No comments:
Post a Comment